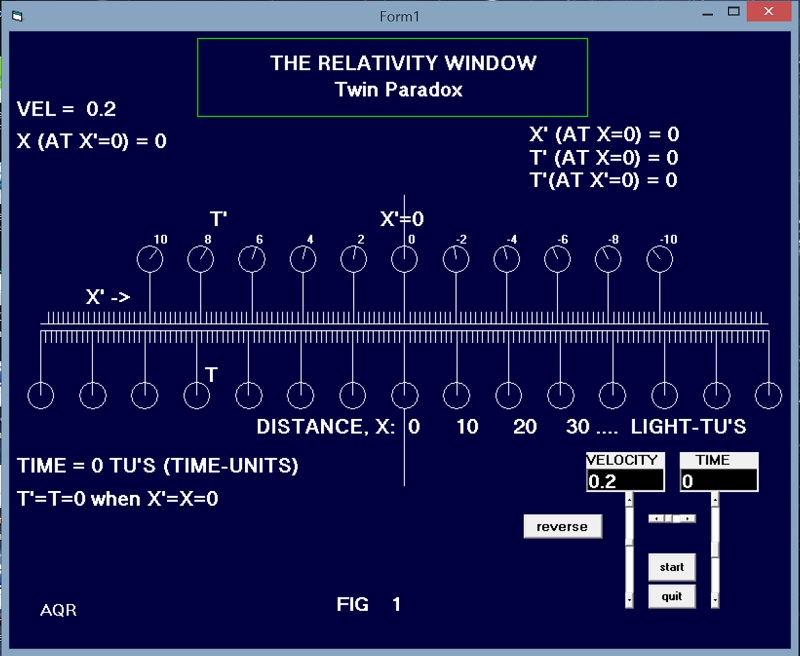
THE TWIN PARADOX The Twin Paradox, sometimes referred to as the Clock Paradox, is frequently used as an attempt to illustrate an error with special relativity. In SR, two frames in motion relative to each other are in a sense equivalent. Viewing the other from either one requires the same transformation of time and length. Thus a dimension on B viewed from A should be exactly the same as the corresponding dimension on A viewed from B. Furthermore, B’s velocity measured in A using A’s instruments is exactly the same as A’s velocity measured in B. Therefore, because of this symmetry, if one member of a set of twins takes a ride on a spaceship then he/she should not gain or lose any time resulting from the trip. Not so. The very short reason is that the space-time paths taken by the twins are not symmetrical with respect to each other as would be required for the elapsed time to remain the same for both frames. Twin A, the traveler, starts on Earth, boards a moving frame for the trip out, then stops and boards another frame in the opposite direction, then finally stops moving (relative to the Earth) and debarks. Twin B, on the other hand simply stays at home and reads a good book. In the following, a twin will travel out for 150 days at 2/10 of the speed of light and return at the same speed. DETAILS OF THE JOURNEY Twin B jumps on a space ship travelling at 0.2c, two-tenths of the speed of light. We can use a version of the “Relativity Window” to visualize the transformations involved. Fig. 1 shows the scene at time zero just after twin B boarded the ship and is travelling to the right at 0.2c. The clocks in our, A’s, frame of reference are seen all synchronized at t = 0. The clocks In B’s frame are seen from our frame with the readings shown. Remember that in B’s frame, B will see synchronized clocks. If a photograph is made in B’s frame at a great distance along an axis perpendicular to the two axes shown with a camera stationary in B’s frame, the clocks in B’s frame will all have the same readings and our clocks will differ. Next, allow twin B to travel for 150 time units. See Fig. 2. As described in the Fermi’s Question section, these views are normalized so that time can be any chosen units. Let’s say one TU is a day so the twin travels for 150 days at 0.2c. At that time we observe that twin B is located at a distance of 30 light-days away and his clock is seen to read 146.97. (146.969)

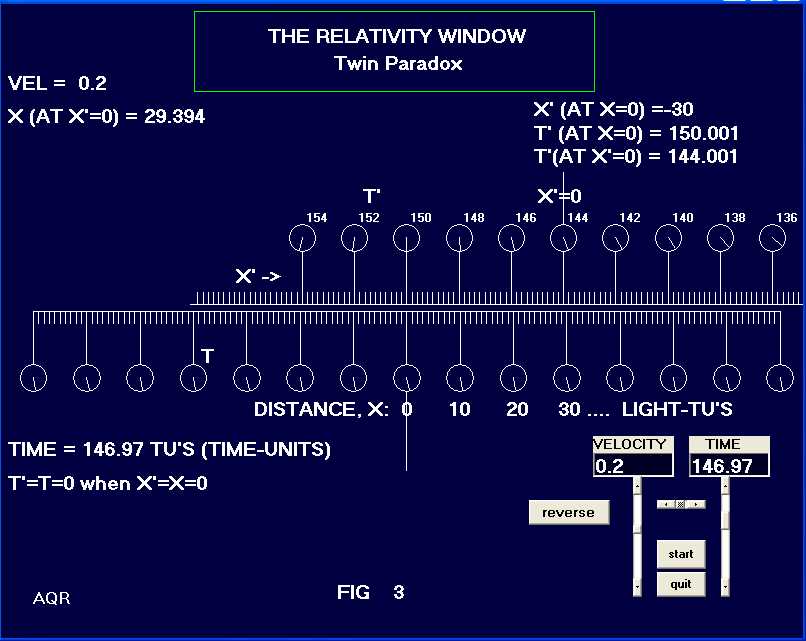
( From twin appendix) (1) t’ = beta (150 - .2 * 30) = 146.969 Where beta = 1.0206 Twin B however, is not concerned with the clock opposite him. He is concerned with the clock of his twin, back at x = 0. He will conduct an observation which is exactly symmetrical to the one described in the previous paragraph. See Fig. 3 in which we adjusted time in the stationary frame to the value 146.97. In Fig. 3 one of B’s clocks reads 150 (days) and is directly opposite x = 0 which is, of course, the location of twin A. This occurs when the clock at x = 0 reads 146.97. From twin B’s viewpoint, all clocks in his frame read the same and so he concludes that his twin’s clock is reading lower than his clock. Note carefully the symmetry here: twin A observes twin B’s clock to be lower than his by exactly the same amount twin B notes A’s clock to be less than his! But the symmetry stops here.

FERMI'S QUESTION HOME PAGE

NEXT PAGE