| 7 | |||||||||||||||||||
| NEXT PAGE | |||||||||||||||||||
| FERMI'S QUESTION HOME | |||||||||||||||||||

|
|||||||||||||||||||

|
|||||||||||||||||||
|
|||||||||||||||||||

|
|||||||||||||||||||
|
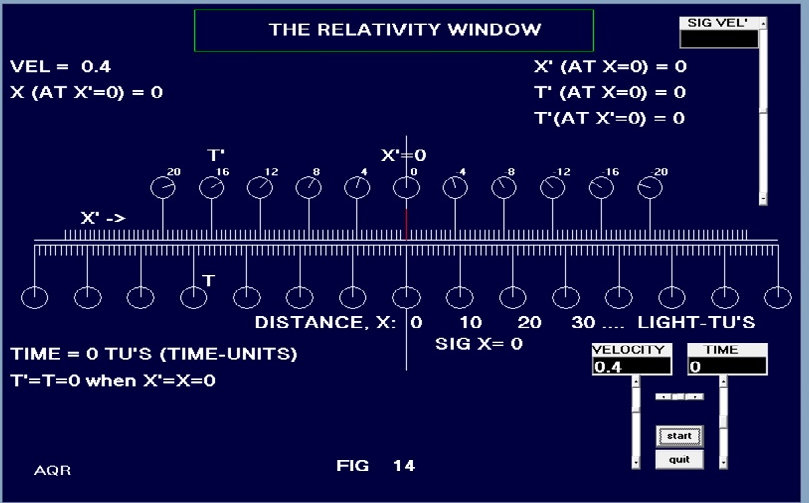
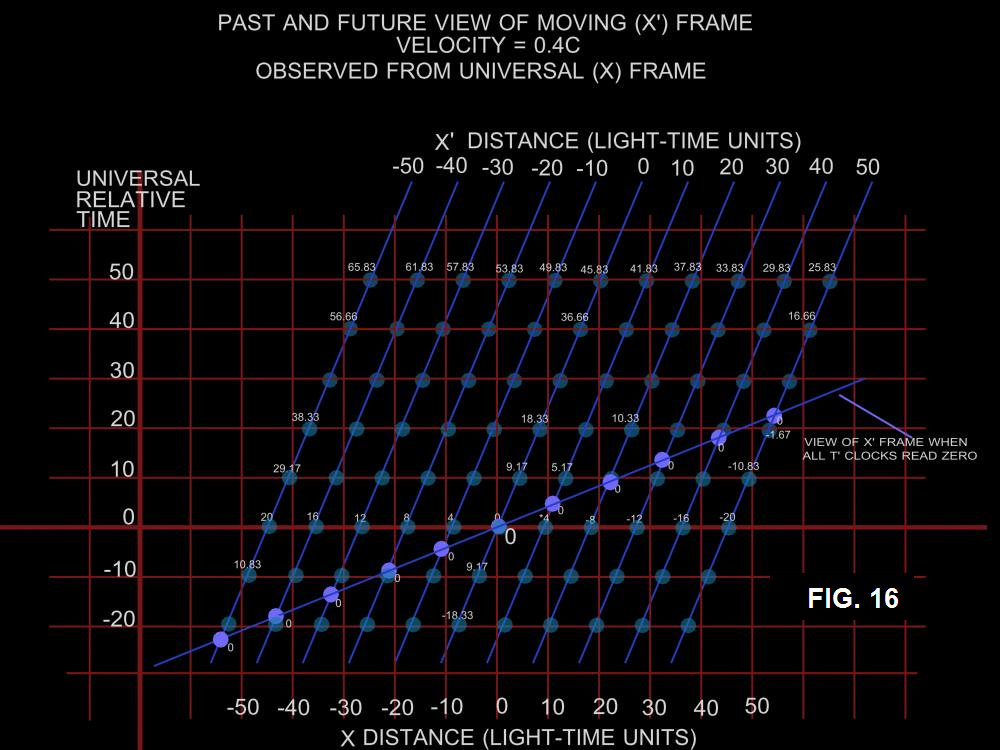
Fig. 15 shows the same relativistic situation but at a different time. Here we can see what happens as time moves ahead. Distance here, as before, is collapsed to a single dimension, X and the time in our frame is 40 TU’s. Question: How can we show the situation from the viewpoint of both systems on one diagram? See Fig. 16. Here the blue shaded lines and circles represent the moving frame. Consider the blue line labeled “view of x’ frame when all t’ clocks read zero”. The blue discs along that line show a “0” next to them which represents the time at those clocks. Thus, in the moving frame, everyone along the blue line (in our past and future) experiences the moment of simultaneous zero time. It seems counter-intuitive that those in the moving frame (along that line), and everyone in our frame at zero time each feel certain of the validity of their own zero time particularly when the clocks in both frames seem so disconnected. |
|||||||||||||||||||
|
|||||||||||||||||||
|
In Fig. 16, the time axis is labeled “Universal Relative Time” and will be explained later. For the present discussion the time axis represents the time in “our” frame and when we experience time=zero TU’s we consider only a horizontal line passing through zero of the time axis. The small blue disks represent the moving frame clocks with clock readings shown next to some of them. The red grid lines provide the time and distance coordinates in “our” frame of reference. Note the correspondence to Fig. 14 taking note of the X distance along the bottom of the image. We are fully aware that the members of the moving frame synchronized their clocks with each other using the very same techniques we used. They are just as confident that their time system is as valid as ours. And yet, it seems that differences are irreconcilable. We set up Fig. 16 in the same way we set up the earlier graphics: We assume that both frames of reference are synchronized such that when the origins of both systems cross each other, the clocks at the two origins read zero. |
|||||||||||||||||||
| NEXT PAGE | |||||||||||||||||||
| FERMI'S QUESTION HOME | |||||||||||||||||||