| NEXT PAGE | ||||||||||||||||||||||||
| HOME | ||||||||||||||||||||||||
| 4 | ||||||||||||||||||||||||
| PREVIOUS PAGE | ||||||||||||||||||||||||
| TACHYONS | ||||||||||||||||||||||||
|
COMMUNICATION WITH FRIENDS AT THE EDGE OF THE SOLAR SYSTEM At a very brief interval before t=0, we send a message from our location at x=0 to a nearby space ship in the X’ frame. That message then gets encoded by our friends in the space ship into a tachyon string (which can be an I-sig in our frame as described earlier). The I-sig is aimed at our friends at x=50 and reaches them at zero time as measured in our frame. For this exercise, let us use units of time as hours. The message is read by our associates, who are located at x=50 light-hours (about 33,500,000,000 miles) out at the edges of our solar system. They are however in our frame of reference. Actually, there was nothing special about the choice of the velocity of the space ship that helped us send that I-sig message by generating an FTL signal in their frame. A single requirement is that their direction is along our negative x axis since we require an FTL signal along the positive x axis. An I-sig would result for any velocity of the other frame if the FTL velocity chosen were the negative reciprocal of the velocity of the space-ship. We wish next to receive a reply from that point located at x=50 light-hours. Consider Fig. 5. Let us now use the same stationary frame as before, but now we consider that the origin is located, for computational simplification, at that distant point 50 light-hours away to the right. We will now, however, use a different adjoining frame, this one going to the right. We are thus now out in space and the Earth is at x= -50 light-hours. We will make use of an adjoining frame which has a velocity of +0.2. This time we establish, within the moving frame, a tachyon with a velocity of -5.0. Thus with the tachyon velocity equal to the negative reciprocal of the frame velocity the requirement for an I signal in our frame, going left, toward Earth, is met. The message encoded tachyons will arrive back at the Earth in zero time and the total message delay will therefore be only the time it took to compose the reply message. |
||||||||||||||||||||||||

|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
| CUSTOMIZING THE I-SIG | ||||||||||||||||||||||||
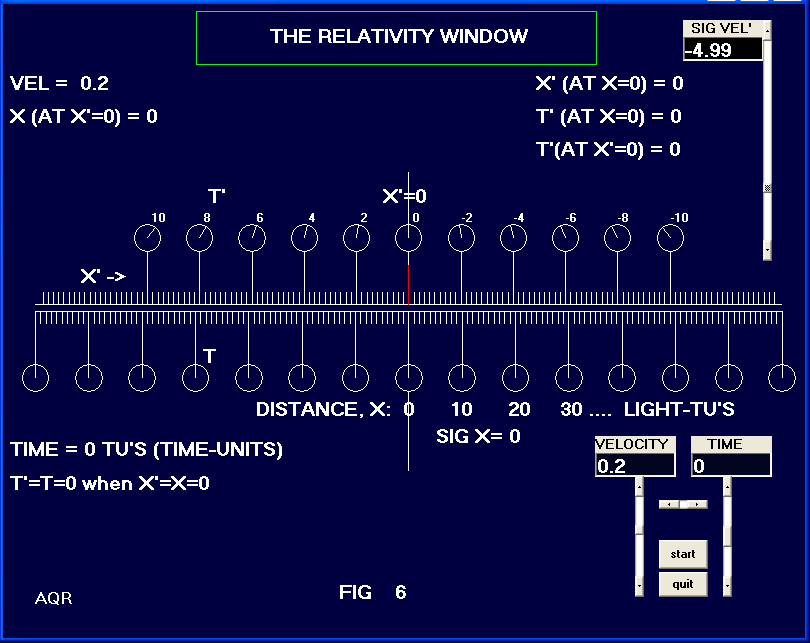
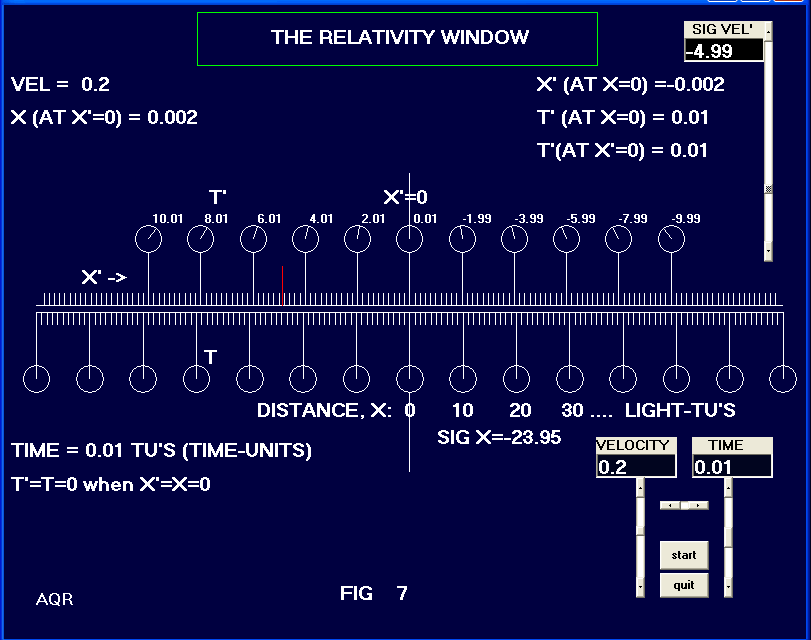
| In order to help us visualize the tachyon’s position and movement we include in Fig. 6 a short vertical red line. That line represents the position of the tachyon at the time of the snapshot. In Fig. 6 we assign a value of -4.99 to the velocity of the tachyon. The tachyon is seen at the origin in both systems, x'=0 and x=0 at our time t=0. The tachyon time is also t’=0 at this moment. Fig. 7 shows the scene for time at 0.01 time-units, or 0.01 hours in our frame. The tachyon has moved to the left and appears at x’=25 light-hours and at a time value of about t’ = 5.01 hours. (time = dist / vel = 25 / 4.99 = 5.01). In Fig. 8 we advance the time in our frame to 0.02 hours and we see the tachyon at approximately x = -50 light-hours or approximately back at Earth. Thus this message time took about 0.02 hours for a round trip by using I-sigs between the Earth and the x=0 point in Fig. 8. Earlier, using Fig. 5 we found that a tachyon in the moving frame, with a velocity of 5 going to the left, would produce an infinitely fast message reply. | ||||||||||||||||||||||||
|
||||||||||||||||||||||||

|
||||||||||||||||||||||||
| We have thus set up an FTL communication system using a conveniently established frame to zip by the remote point at the right time to receive the reply signal and to rebroadcast it as a left going FTL signal. | ||||||||||||||||||||||||
| NEXT PAGE | ||||||||||||||||||||||||
| HOME | ||||||||||||||||||||||||
| PREVIOUS PAGE | ||||||||||||||||||||||||