2

THE RELATIVITY WINDOW

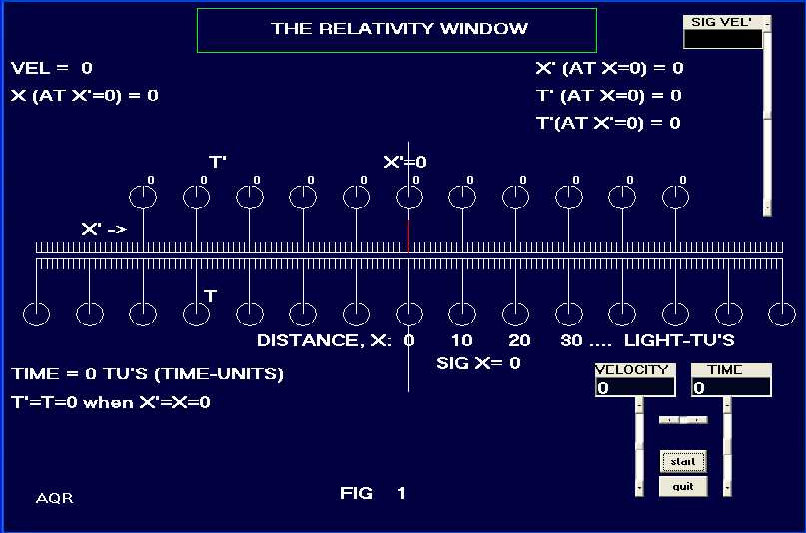
We can provide a nice visual representation of how special relativity makes the world look. See Fig. 1. Ignoring the scroll bars at the right side of the figure, the upper half represents the O’, the moving frame, and the lower half the O frame, --- OUR --- frame at rest. The view here is at the initial rest position. The primed frame, O’, is not in motion in this figure and its origin (shown at x’=0) at this time coincides with the origin of the O frame at x=0. The circles represent clocks; 11 clocks are shown for the O’ frame, and 15 for the O frame. One rotation of the hand on the clocks is 100 units of time, whatever time unit you choose. The clocks are separated by ten distance units, as perhaps ten light-seconds, or ten light-years --- in general as light-TU’s --- light-timeunits. The O’ clocks have their face readings shown next to the clocks. In the initial rest position, all clocks read zero, and x’=0 is directly opposite x=0.

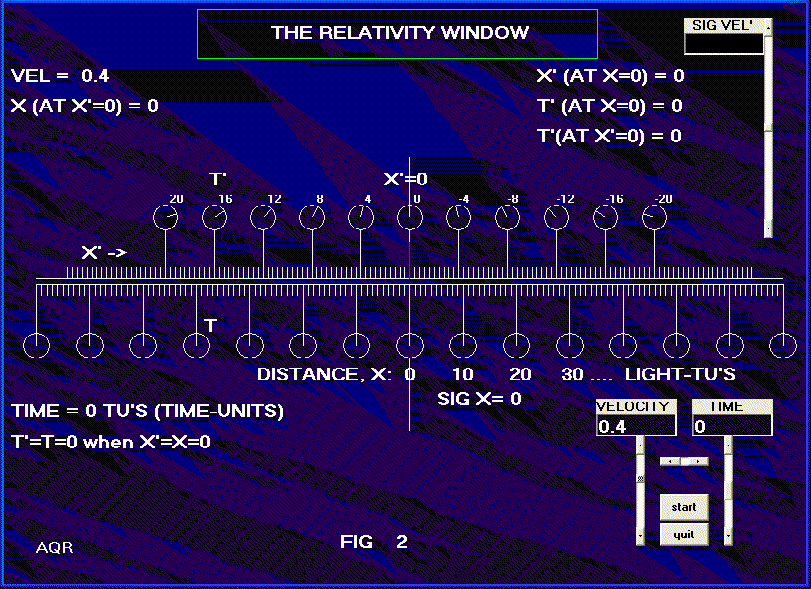
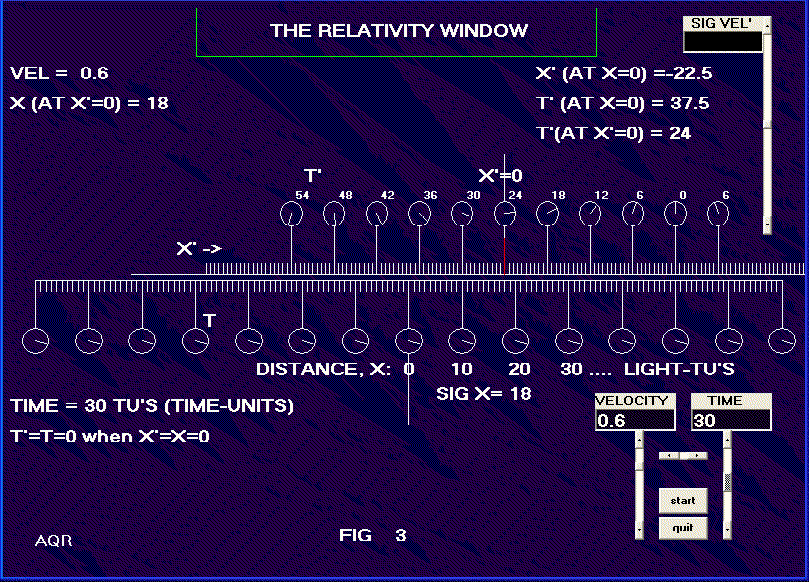
When O’ is in motion, the assumption is made that at the instant when x’=0 is opposite x=0, the clock located at x’=0 will read t’=0. All clocks in the stationary frame, O, will also at that moment read zero. See for example, Fig. 2, showing a velocity of 0.4 meaning the velocity is four tenths of the speed of light.

Note that there are shown ten divisions between each of the clocks. Thus in the moving frame, at the point x’=20, the time in the moving frame, t’, equals -8. If we were using years as the time unit, then x’ at that point would be 20 light-years.

Notice in Fig. 2 the relativistic effect of the speed. Note the readings on the clocks at the various values of x’, and note the fact that x’ distances are now shorter than the x distances as viewed, of course, from our frame, the O frame.

Fig. 3 shows the situation for a velocity of 0.6, and with the time in the stationary frame set to 30. The point, x = 50 light-TU’s is directly opposite x’ = 40 light-TU’s and the clock there shows t’=0. Note that distances in the moving frame are shorter than corresponding distances in the stationary frame as seen from the stationary frame. Note particularly the time on the other clocks. Some are earlier and some later than the time in our frame. Note that the clocks in the moving frame were synchronized, as per convention, in the same manner as the clocks in our frame --- and they all have the same reading simultaneously when viewed in the other frame --- yet no two of the moving clocks read the same as seen from our frame. The observance of simultaneity does not transfer between relatively moving frames.

The picture of time and distance between two moving frames of reference, as seen through our "Relativity Window", looks very unfamiliar in terms of everyday life. It should be noted that the transformations apply not just to light, but to all matter, anything, which can be defined by distance and time.

A question might be raised as to the validity of a "picture" of the scene as depicted in the figures. A picture, after all, uses light itself and that light takes different amounts of time to reach the lens of a camera from different parts of the scene. We can overcome this objection by locating our camera somewhere along the Z axis, (coming out of the page) and far enough distant that there is negligible difference in distance from the camera to either side of the x axis within the view.

NEXT PAGE

HOME